信号
声音是一种信号(signal)。
声音是空气压力变化产生,声音信号则代表着空气压力随时间的变化。麦克风能够测量这种变化并转换成可以表示声音的电信号。扬声器可以接收这种电信号并产生相应的声音。
下图是一段正弦信号,横坐标是时间,纵坐标是信号强度。
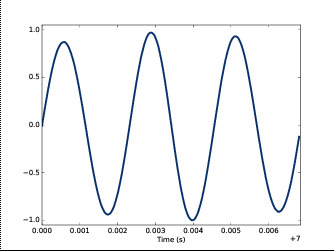
这个信号有三个重复循环(cycle)信号,周期(peroid)是一个cycle的时间,频率(frequence)是信号每秒cycle的个数。
波形图
对声音信号以采样率N进行采样,可以得到声音信号在时域上的信息,信号在时域上的强度图称为信号的波形(waveform)。波形图能够表达声音信号的时域信息。波形图横坐标是时间,纵坐标表示信号在该时间序列上的值,其中每个时间点叫做帧(frame),也可以叫做采样(sample)。采样率是指每秒从连续声音信号中提取并组成离散信号的采样个数,用赫兹(Hz)来表示。两次采样之间的时间间隔称为时间步长(timestep),为采样率的倒数。
tacotron和SV中,声音文件预处理采样率为16000hz时,时间步长为0.0625ms。声音频率为440hz时候,每个cycle周期为2.273ms,每个cycle里有36个采样点。根据采样定理可知,我们处理声音信号的时候,要注意我们选择的采样率应该大于等于录音中正常声音的最大频率的两倍,采样值就可以包含原始信号的所有信息,被采样的信号就可以不失真的还原成原始信号。因为
采样周期的整数倍时相位重合。
下面的代码能够生成上图的波形。
import numpy as np
import math
N = 16000
fs = 440
x = np.linspace(0,1,N)
y = [math.sin(2*math.pi*fs*t/N) for t in range(N)]
读写波形数据可以使用librosa模块或者scipy模块。
- 用librosa模块读写波形数据。
#读取波形数据:路径为fpath_or_wav,sr为采样率,保存到wav里 #librosa.core.load(path, sr=22050, mono=True, offset=0.0, duration=None, dtype=<class #'numpy.float32'>, res_type='kaiser_best') import librosa wav, source_sr = librosa.load(fpath_or_wav, sr=None) #写波形数据,把波形以sr的采样率存储到path路径下,y是波形数据。 librosa.output.write_wav(path,y,sr) - 用scipy模块读写波形数据,注意read时返回wav只能时以int形式。
#读取波形数据:路径为fpath_or_wav,sr为采样率,保存到wav里 #scipy.io.wavfile.read(filename,mmap=False) #filename: string or open file handle #mmap:whether to read data as memory mapped import scipy source_sr,wav = scipy.io.wavfile.read (fpath_or_wav, sr=None) #写波形数据,把波形以rate的采样率存储到filename路径下,data是波形数据(可以是float32,int32PCM,int16PCM,int8PCM)。 scipy.io.wavfile.write(filename,rate,data)下图是小提琴演奏中截取的一部分录音的波形。
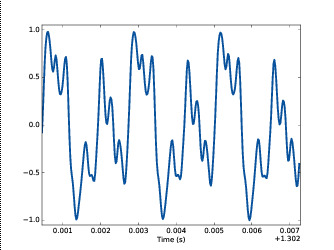
频谱分解
信号可以进行频谱分解是由于信号可以表示为不同频率的正弦信号的叠加结果, 这些不同频率的正弦信号的集合就是频谱(spectrum)。信号经过傅立叶变换就可以得到它的频谱。 傅里叶变换:
根据欧拉公式,积分部分可以写为:
实际上正弦和余弦相当于标准正交基的组合。
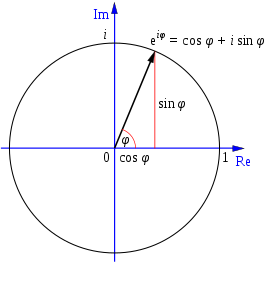
而根据傅里叶级数告诉我们任何的周期信号都能写成下面这种形式:
理解:用正弦余弦正交基把相同频率的信号给摘选出来了,不同频率的的过滤掉了。 傅立叶变换实际上是分解声音的过程,人听声音就是这样,能够自动摘出这种信息,从而知道讲话的人是谁。 NumPy中,fft模块提供了快速傅里叶变换(傅里叶变化的一种揭发,利用分治的思想)的功能。fft和ifft傅里叶变换和逆变换。
import numpy as np
x = np.linspace(0, 2 * np.pi, 30) #创建一个包含30个点的余弦波信号
wave = np.cos(x)
transformed = np.fft.fft(wave) #使用fft函数对余弦波信号进行傅里叶变换。
np.all(np.abs(np.fft.ifft(transformed) - wave) < 10 ** -9) #对变换后的结果应用ifft函数,应该可以近似地还原初始信号。
下图是小提琴声音的频谱。其中x轴代表了组成这个信号的正弦波频率的范围, y轴显示了它们的强度(也叫做幅度)。
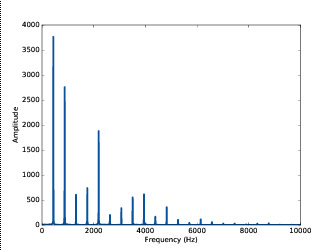
频谱中最小的频率称作基频。幅度最大的频率称作 主导频率。我们对音高的感受取决于声音的基频(即使它不是主导频率)。这个信号的基频和主导频率都是440Hz。频谱中其他幅度比较大的频率是880Hz,1320Hz,1760Hz和2200Hz,它们都是基频的整数倍,这些频率分量称为信号的谐波(harmonics)。在基于参数的语音合成系统中,基频作废重要的语音学特征,是一个非常重要的预测参数。
声谱图
频谱图展示的是整个时间段内的频率分解,我们从中读不到每个时刻的情况。为了展示信号频率随时间变化的关系,把信号分段后分别计算频谱,然后画出每段的频谱图,这就是声谱图。 这种方法是 短时傅立叶变换(STFT) 。他的思想大概是:把长的非平稳随机过程看成是一系列短时随机平稳信号的叠加,短时性可通过在时间上加窗口函数实现。 具体实现则是通过在傅立叶变换中,使用时间窗口函数g(t−u)与源信号f(t)相乘,实现在u附近的加窗口和平移,然后进行傅立叶变换。
下面是librosa中短时傅里叶变换stft处理代码的演示:
y, sr = librosa.load(librosa.util.example_audio_file())
print(np.abs(librosa.stft(y)))
array([[2.58028018e-03, 4.32422794e-02, 6.61255598e-01, ...,6.82710262e-04, 2.51654536e-04, 7.23036574e-05],
[2.49403086e-03, 5.15930466e-02, 6.00107312e-01, ...,3.48026224e-04, 2.35853557e-04, 7.54836728e-05],
[7.82410789e-04, 1.05394892e-01, 4.37517226e-01, ...,6.29352580e-04, 3.38571583e-04, 8.38094638e-05],
...,
[9.48568513e-08, 4.74725084e-07, 1.50052492e-05, ...,1.85637656e-08, 2.89708542e-08, 5.74304337e-09],
[1.25165826e-07, 8.58259284e-07, 1.11157215e-05, ...,3.49099771e-08, 3.11740926e-08, 5.29926236e-09],
[1.70630571e-07, 8.92518756e-07, 1.23656537e-05, ...,5.33256745e-08, 3.33264900e-08, 5.13272980e-09]], dtype=float32)
下图是一段频率平稳上升的声谱图.随着时间推进频率逐渐增加的一段频谱图,横坐标为时间,纵坐标为频率,颜色代表幅值。
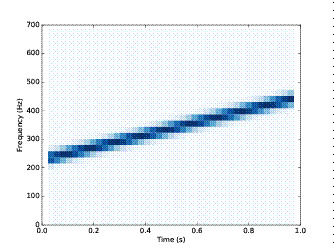
梅尔谱(mel spectrogram)
梅尔尺度是建立从人类的听觉感知的频率—Pitch到声音实际频率直接的映射。人耳对于低频声音的分辨率要高于高频的声音。通过把频率转换成梅尔尺度,我们的特征能够更好的匹配人类的听觉感知效果。从频率到美尔频率的转换公式如下:
下图是声谱图到梅尔谱映射。Hz到mel的映射图,由于它们是log的关系,当频率较小时,mel随Hz变化较快;当频率很大时,mel的上升很缓慢,曲线的斜率很小。这说明了人耳对低频音调的感知较灵敏,在高频时人耳是很迟钝的,梅尔标度滤波器组启发于此。
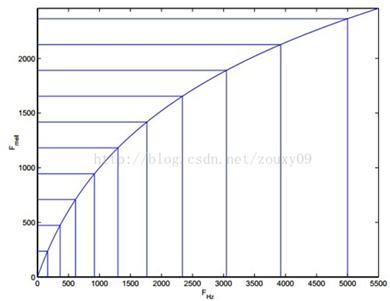
下图是等面积梅尔滤波器。如图所示,40个三角滤波器组成滤波器组,低频处滤波器密集,门限值大,高频处滤波器稀疏,门限值低。恰好对应了频率越高人耳越迟钝这一客观规律。图6所示的滤波器形式叫做等面积梅尔滤波器(Mel-filter bank with same bank area),在人声领域(语音识别,说话人辨认)等领域应用广泛,但是如果用到非人声领域,就会丢掉很多高频信息。这时我们使用等高梅尔滤波器,图7。
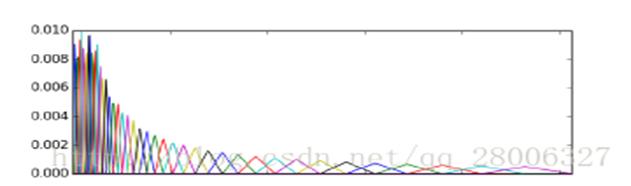
下图是等高梅尔滤波器。SV中预处理时使用了40个等面积梅尔滤波器梅尔滤波器组,滤波器组中的每个滤波器都是一个三角形,在中心频率处的值为1,并向0线性减小,直到到达值为0,也是下一个相邻滤波器的中心频率。
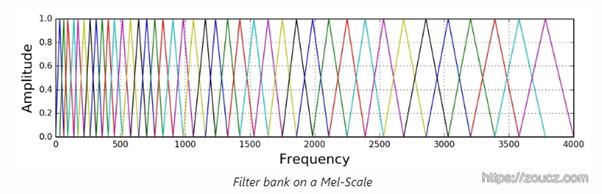
Librosa中实现从音频文件到梅尔谱的方法:
y, sr = librosa.load(librosa.util.example_audio_file())
print(librosa.feature.melspectrogram(y=y, sr=sr))
array([[ 2.891e-07, 2.548e-03, ..., 8.116e-09, 5.633e-09],
[ 1.986e-07, 1.162e-02, ..., 9.332e-08, 6.716e-09],
...,
[ 3.668e-09, 2.029e-08, ..., 3.208e-09, 2.864e-09],
[ 2.561e-10, 2.096e-09, ..., 7.543e-10, 6.101e-10]])
采样定理
采样是本身是将一个信号(例如时间或空间上连续的函数)转换为数字序列(时间或空间上离散的函数)的过程。 采样定理指出,如果週期函數 x(t) 不包含高于 B cps(次/秒)的频率,那麼,一系列小於 1/(2B) 秒的x(t)函數值將會受到前一個週期的x(t)函數值影響。因此 2B 样本/秒或更高的采样频率將能使函數不受干擾。相對的,对于一个给定的采样频率 f,完全重构的频带限制为 B ≤ f/2。 如果不能满足上述采样条件,采样后信号的频率就会重叠,即高于采样频率一半的频率成分将被重建成低于采样频率一半的信号。这种频谱的重叠导致的失真称为混叠,而重建出来的信号称为原信号的混叠替身,因为这两个信号有同样的样本值。