支持向量机 SVM Support Vector Machine 最优化 核方法 kernel method 对偶 拉格朗日乘子法 KKT条件

支持向量机

Support Vector Machine

Posted by 朱晓旭 on March 10, 2020

支持向量机

简介

支持向量机(support vector machine)是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。 以上是维基百科的对SVM的定义。
用通俗的话讲，它是一种统计机器学习的分类方法，根据训练集分布去寻找一个最大间隔超平面。1963年被提出，92年通过核方法可以实现非线性分类。 在支持向量机被普遍接受后，核技巧(kernel trick) 被人们用到了机器学习的几乎每一个角落，核方法也逐渐成为 机器学习的基本内容之一。 支持向量机在分类问题中有着重要地位，其主要思想是最大化两类之间的间隔。按照数据集的特点我们采用的不同算法：

  1. 对于线性可分问题，采用hard-margin SVM。
  2. 对于允许少部分错误点的线性可分问题，采用soft-margin SVM。
  3. 对于非线性问题，完全不可分，采用kernel method。

hard-margin SVM

margin and sv

给定训练样本data:

$$\{(x_{i},y_{i})\}_{i=1}^{N}$$
$$y_{i}\in\{1,-1\},x_{i}\in{\mathbb{R}}^{d}$$

分类器的预测目标是：给定x情况下，预测y属于哪类。 分类学习最基本的想法就是基于训练集data在样本空间中找到一个划分超平面，将不同类别的样本分开。 在样本空间中，划分超平面可以通过下面的线性方程描述：

$$w^{T}x_{i}+b=0$$

$w=(w_{1};w_{2};…;w_{d})$是法向量，决定了超平面的方向；b是位移项，决定了超平面与原点之间的距离。划分超平面可被法向量和位移项唯一的确定。 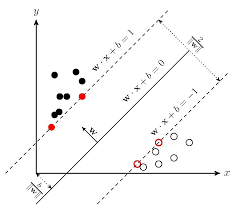实现分类超平面的约束条件则是(其中1代表正类，-1代表反类)：

$$w^{T}x_{i}+b>0,y_{i}=1$$
$$w^{T}x_{i}+b<0,y_{i}=-1$$

即：

$$y_{i}(w^{T}x_{i}+b)>0,i \in \{1,2,3...,N\} $$

而从下图可以看到，能把训练样本分开的划分超平面可能有很多。
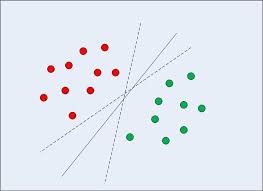我们应该努力寻找的应该是距离两者最中间的那条实线，因为它对噪声的容忍最好，也就是说它的鲁棒性更好，对集外的样本泛化能力更强。距离样本点最近的点与超平面的距离是所有平面中最大的。它就是最大间隔超平面：

统计学习方法对margin的理解

在超平面$w^{T}x_{i}+b=0$确定的情况下，$|w^{T}x_{i}+b|$能够相对的表示采样点距离超平面的远近，而通过判断$w^{T}x_{i}+b$的符号是否与$y_{i}$一致可以判断分类是否正确。所以可以用$y_{i}(w^{T}x_{i}+b)$代表分类的正确性与确信度。这就是函数间隔的定义：

$$FucntionalMargin = y_{i}(w^{T}x_{i}+b)$$

这样定义存在一个问题，同比例的改变法向量w和位移项的值(比如2w，2b)，超平面没有改变，间隔却变成原来的两倍。因此我们可以对划分超平面的法向量加以约束(如规范化，${\left|w\right|_2}=1$),这时函数间隔变成几何间隔(geometric margin)。我们以此定义距离的远近。

$$GeometricMargin = \frac{y_{i}(w^{T}x_{i}+b)}{\left\|w\right\|_2}$$

同样的，几何间隔能够代表分类的正确性与确信度。正确性体现在符号，确信度体现在distance。x为二维时，实际上就是点到直线的距离；x为高维时，指的是采样点到超平面的距离。
我们所指的margin是支持向量的margin，其中支持向量是geometric margin最小的采样点。

周志华的机器学习对margin的理解

两个异类的支持向量到超平面的距离之和为margin，也就是两条直线之间的距离，如下图所示：

$$margin = \frac{2}{\left\|w\right\|_2}$$

欲找到具有”最大间隔” (maximum margin)的划分超平面，也就是要找到能满足约束参数w和b的同时，使得margin最大。

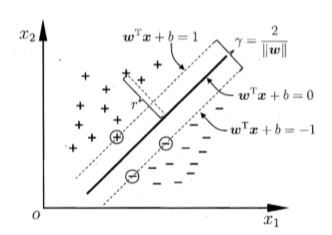
约束优化问题

由此，分类问题转化为了约束优化问题:

$$ \max_{w,b}\min_{x_{i},i \in \{1,2,3..N\}}\frac{1}{\left\|w\right\|_2}y_{i}(w^{T}x_{i}+b)=\max_{w,b}\frac{1}{\left\|w\right\|_2}\min_{x_{i},i \in \{1,2,3..N\}}y_{i}(w^{T}x_{i}+b)$$
$$s.t. y_{i}(w^{T}x_{i}+b)>0$$

这样的话：

$$\max_{w,b}\frac{1}{\left\|w\right\|_2}$$
$$s.t. \min y_{i}(w^{T}x_{i}+b)=1 $$

统计学习方法解释：函数间隔r的取值并不影响最优化问题的解。事实上，假设将w和b按照比例改编为nw和nb，这时函数间隔变为nr。函数间隔的这一改变对上面问题的不等式约束没有影响，对目标函数优化也没有影响，也就是说改变r，产生的是一个等价的最优化问题。

理解：

$${\exists}{r>0}, s.t. \min_{x_{i},y_{i},i \in \{1,2,3,4...N\}}y_{i}(w^{T}x_{i}+b)=r $$

而r的取值可以是任意大于零的数，为了方便计算，此处取为1。

我们在求解最优化问题时，往往采用最小化,最大化间隔相当于最小化$\frac{1}{2}w^{T}w$：

$$\min_{w,b}\frac{1}{2}w^{T}w$$
$$s.t. \min y_{i}(w^{T}x_{i}+b)=1 $$

这是注意到问题本身是一个凸二次规划(convex quadratic programming)问题，能直接用现成的优化计算包求解，但我们可以有更高效的办法。

拉格朗日乘子法与对偶技巧

对于带约束的优化问题，我们应用拉格朗日乘子法

$$ L(w,b,a)=\frac{1}{2}w^{T}w+\sum_{i=1}^{N}a_{i}(1-y_{i}(w^{T}x_{i}+b))$$

其中，a是N维的向量。 因此：

$$\min_{w,b}\max_{a}L(w,b,a)$$
$$s.t. a>=0 $$

理解为什么a>=0(数学角度上是KKT条件，此处常理分析):
如果$(1-y_{i}(w^{T}x_{i}+b))>0$,a可以是大于0的任意一个数，那$\max_{a}L(w,b,a)$本身是没有意义的。
如果$(1-y_{i}(w^{T}x_{i}+b))<=0$,a取0，才和原式恒等。
为了求解线性可分支持向量机的最优化问题，将它作为原始最优化问题，应用拉格朗日对偶性通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解。

$$\max_{a}\min_{w,b}L(w,b,a)$$
$$s.t. a_{i}>=0 $$

为什么把原问题转换为对偶问题：一是对偶问题更容易求解(通过拉格朗日乘子法抛弃约束给a，因此可以可以通过求偏导求解$\min_{w,b}L(w,b,a)$,此使把a看作常量),二是自然引入核函数，进而推广到非线性问题。
由统计学习方法-李航第225页的附录C拉格朗日对偶性中定理C.3可知为强对偶的充要条件是满足KKT条件。
KKT条件(原问题和对偶问题具有强对偶关系的充要条件)：

$$\frac{\partial{L}}{\partial{w}}=0$$
$$\frac{\partial{L}}{\partial{b}}=0$$
$$\frac{\partial{L}}{\partial{a}}=0$$
$$a_{i}>=0$$
$$1-y_{i}(w^{T}x_{i}+b)<=0$$
$$a_{i}(1-y_{i}(w^{T}x_{i}+b))=0$$

问题求解

为了得到对偶问题的解，先求L(w,b,a)对w，b的极小，再求对a的极大。 对w,b求偏导得:

$$\sum_{i=1}^{N}a_{i}y_{i}=0$$
$$w=\sum_{i=1}^{N}a_{i}y_{i}x_{i}$$

把结果带入对偶式，得：

$$\max_{a}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_{i}a_{j}y_{i}y_{j}x_{i}^{T}x_{j}+\sum_{i=1}^{N}a_{i}$$
$$s.t. a_{i}>=0 , \sum_{i=1}^{N}a_{i}y_{i}=0 $$

然后转为最小化问题：

$$\min_{a}\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_{i}a_{j}y_{i}y_{j}x_{i}^{T}x_{j}-\sum_{i=1}^{N}a_{i}$$
$$s.t. a_{i}>=0 , \sum_{i=1}^{N}a_{i}y_{i}=0 $$

可以求解a(统计学习方法中介绍SMO)。 其中$w^{*}$在对L求导时已经求出：

$$w^{*}=\sum_{i=1}^{N}a_{i}y_{i}x_{i}$$

由KKT条件的后三个，只要样本点不是支持向量，$a_{i}$必须为0。
对于支持向量$x_{s},y_{s}$,其$1-y_{s}\left( w^{T}x_{s}+ b^{*} \right)=0$。
由此可得：

$$b^{*}=y_{s}-\sum_{i=1}^{N}a_{i}y_{i}x_{i}^{T}x_{s}$$

因此，原问题的解也为：

$$w^{*}=\sum_{i=1}^{N}a_{i}y_{i}x_{i}$$
$$b^{*}=y_{s}-\sum_{i=1}^{N}a_{i}y_{i}x_{i}^{T}x_{s}$$

因此得到我们的划分超平面为：

$$f(x)= \sum_{i=1}^{N}a_{i}y_{i}x_{i}^{T}x+y_{s}-\sum_{i=1}^{N}a_{i}y_{i}x_{i}^{T}x_{s}$$

soft-margin SVM

当存在噪声样本时，训练集的样本集并不能被严格地线性可分(即使使用了后面的核函数)。如果按照原来的约束条件进行求解，会使得整个问题无解。hard margin分类，硬性的要求所有的样本点都满足和分类平面间距离必须大于某个值。
软间隔同样是针对线性可分问题。它的核心思想是：允许少许错误。 适用soft margin的情况：当数据存在噪声的时候用软间隔。

$$\min_{w,b}\frac{1}{2}w^{T}w + loss$$

loss可以是分错的数量乘以系数C(系数C用来控制惩罚力度)，使用0/1损失函数或者铰链损失函数。它的原理实质上和深度学习的正则化类似。
加入loss后目标函数多一个正则项，约束条件对每个样本多了一个松弛变量。每个样本数据都有一个对应的松弛变量，用以表示该样本不满足约束的程度。 此

$$\min_{w,b}\frac{1}{2}w^{T}w+C\sum_{i=1}^{N}\xi{_{i}}$$

$$s.t. y_{i}(w^{T}x_{i}+b)>=1-\xi_{i} ,\xi_{i}>=0$$

kernel Method

维度转换

我们假设训练样本是线性可分的，即存在一个划分超平面能将训练样本正确分类。而对于数据本身线性不可分的情况，无法用线性模型将正负例分开。 然而低维线性不可分的输入空间进行高维映射，往往在高维更易线性可分。高维映射不仅仅用于svm，还应用于线性回归，逻辑回归等。可以看下面的例子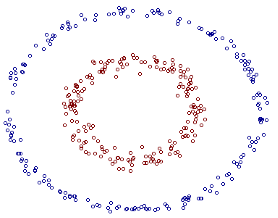： 二维平面上的点无法用一条直线分开，可以将其按照一定规则映射到三维空间中，可以用超平面将其分开。 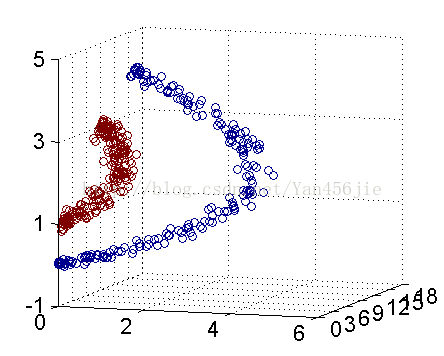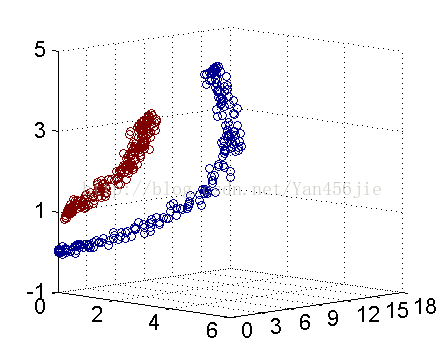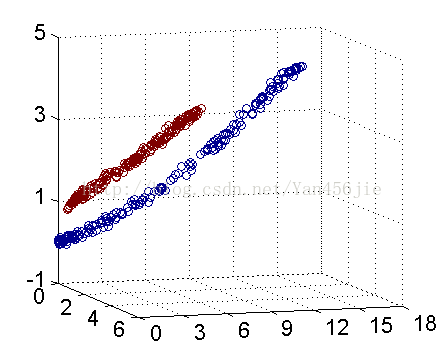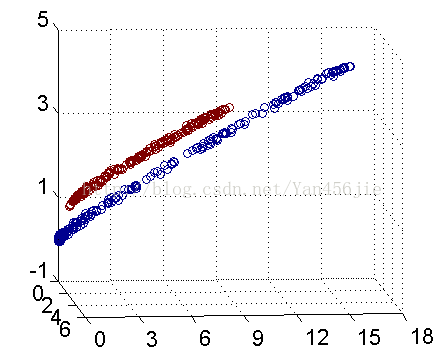维度转换： 设原空间为$X\subset{\mathbb{R}}^{d},x_{i}\in{X}$,新空间为$Z\subset{\mathbb{R}}^{d},z_{i}\in{Z}$

$$z_{i} = \phi(x_{i})$$

带来的问题

维度转换后在hard-margin svm中的对偶问题是：

$$\max_{a}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_{i}a_{j}y_{i}y_{j}\phi({x_{i}^{T}})\phi({x_{j}})-\sum_{i=1}^{N}a_{i}$$
$$s.t. a_{i}>=0 , \sum_{i=1}^{N}a_{i}y_{i}=0 $$

由此带来的问题是对偶问题带来的内积表示:

$$\phi({x_{i}^{T}})\phi({x_{j}})$$

由于特征空间维数可能很高，甚至可能是无穷维，因此直接计算内积是非常困难的。

核方法

为了避免高维空间的内积计算，我们可以设想这样一个函数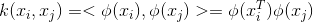： 即$x_{i},x_{j}$维度转换后在高维空间的内积等于他们在原始空间通过函数$k(x_{i},x_{j})$计算的结果。有了这样的函数，我们就不必直接去计算高维甚至无穷维特征空间中的内积，维度转换后的对偶问题可以表示为：

$$\max_{a}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_{i}a_{j}y_{i}y_{j}k(x_{i},x_{j})-\sum_{i=1}^{N}a_{i}$$
$$s.t. a_{i}>=0 , \sum_{i=1}^{N}a_{i}y_{i}=0 $$

求解后即得：

$$f(x)= \sum_{i=1}^{N}a_{i}y_{i}k(x_{i},x)+y_{s}-\sum_{i=1}^{N}a_{i}y_{i}k(x_{i},x_{s})$$

上述的k函数就是核函数。周志华的机器学习中给出核函数的定义是： 只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。事实上，对于一个半正定核矩阵，总能找到一个与之对应的映射$\phi$。
不同的核函数对应高维映射不同，数据的分布情况不同，直接影响着分类质量。若是映射到一个不合适的空间那么很可能导致性能不佳。

另外，该书中指出：核函数的线性组合仍然是核函数；核函数的乘积仍然是核函数；核函数和其他函数的乘积仍然是核函数。

我们使用的时候一般通过查表的方法选择合适的核函数。
其中第一个是处理线性可分问题的，也就是不使用核方法或者说使用线性核。真正处理的时候，我们会优先选择线性核，如果效果不好的时候，考虑尝试其他核函数。

代码实现

基于SMO算法实现hard margin。代码摘自github

import numpy as np
from sympy import *

class supprot_vector_machine:
    def __init__(self, feature, label):
        self.feature = np.array(feature)										
        self.label =  np.array(label)											
        self.N = len(self.feature)												
        self.n = -1			
        self.alpha = symbols(["alpha" + str(i) for i in range(1, self.N + 1)])	
        self.solution = []														

    def transvection(self, a,b): 
        result = 0 
        offset = len(a)
        for i in range(offset):
            result += a[i] * b[i]
        return result

    def eval_function(self): 
        c = 0
        s = 0 
        offset = self.N
        for i in range(offset):
            s += self.alpha[i]
            for j in range(offset):
                c += self.alpha[i] * self.alpha[j] * self.label[i][0] * self.label[j][0] * self.transvection(self.feature[i], self.feature[j])
        self.equation = c/2 - s

    def replace_x(self): 
        self.n+=1
        alpha_ = self.alpha[:]
        for i in range(len(alpha_)):
            alpha_[i] = alpha_[i] * self.label[i][0]							
        equation = Eq(sum(alpha_),0)											  
		self.solve_equation =  solve([equation], self.alpha[0])					
		self.equation = self.equation.replace(self.solve_equation.keys()[0],	
                                              self.solve_equation.get(self.solve_equation.keys()[0])) 

	def derivative(self): 
        self.surplus_alpha = self.alpha[:]										
        self.equation_list = []
        self.surplus_alpha.remove(self.solve_equation.keys()[0])				
        for i in self.surplus_alpha:
            self.equation_list.append(diff(self.equation, i))					
        self.solution = solve(self.equation_list)								

    def boundary(self): 
        min = 10000
        self.surplus_alpha.reverse()										

        s = solve(self.replace_model(self.equation_list[:]))

        finaly = []
        for i in range(len(s)):
            m = self.equation
            for j in range(len(s)):
                if j!=i:
                    m = m.replace(symbols("alpha"+str(j+2)), 0)
            finaly.append(m)

        for i in range(len(s)):
            K = Eq(symbols("pp"), finaly[i])
            sad = solve([K, Eq(symbols("alpha" + str(i+2)), s.get(symbols("alpha" + str(i+2))))])[0].get(symbols("pp"))
            if min > sad:
                result = {}
                min = sad
                result[symbols("alpha" + str(i+2))] = s.get(symbols("alpha" + str(i+2)))

        for i in range(2, len(s)+2):
            if symbols("alpha"+str(i)) not in result.keys():
                result[symbols("alpha"+str(i))] = 0

        self.solution = result

    def replace_model(self, lists):
        bound = lists
        k=len(bound)
        for i in range(k):
            for j in range(k):
                if j!=i:
                    bound[i] = bound[i].replace(symbols("alpha"+str(j+2)), 0)
        return bound

    def get_origin(self, source):
        value_list = [Eq(i, source.get(i)) for i in source.keys()]
        value_list.append(Eq(self.solve_equation.keys()[0], self.solve_equation.get(self.solve_equation.keys()[0])))
        return solve(value_list)

    def fit(self):															
        self.eval_function()
        self.replace_x()
        self.derivative()
        for i in self.solution:
            if (self.solution.get(i)) < 0:
                self.boundary()
                break
        if self.solution == []:
            self.boundary()
        self.solution = self.get_origin(self.solution)

        final_alpha = [self.solution.get(self.alpha[i]) for i in range(len(self.solution))]
        final_alpha = [[i] for i in final_alpha]


        self.w = sum(final_alpha *self.feature*self.label)

        for i in range(len(final_alpha)): 
            if final_alpha[i] != 0:
                alpha_j = i
                break
        kk = []
        for i in range(self.N):
            kk.append(self.transvection(self.feature[i], self.feature[alpha_j]))

        self.b = [final_alpha[i] * self.label[i] * kk[i] for i in range(self.N)]
        self.b = self.label[alpha_j] - sum(self.b)
																
    def prediction(self, feature):
        Mat = np.array(feature).transpose()
        col = Mat.shape[1]

        output = []
        for i in range(col):
            if sum(Mat[:,i] * self.w) + self.b > 0:
                output.append(+1)
            else:
                output.append(-1)

        return output

总结

  1. 支持向量机能够解决线性可分问题，线性可分带有容错率问题以及线性不可分问题。
  2. 支持向量机的核心是求解最优划分超平面，而划分超平面由少数的支持向量所确定，而不是样本空间的维数,这在某种意义上避免了“维数灾难”。
  3. 对偶表示带来内积，对于线性不可分数据进行高维映射后带来计算困难，核方法巧妙的把高维空间的内积通过核函数表达，大大减小了计算量。
  4. 传统支持向量机只针对二分类问题，对于多分类问题要通过组合多个支持向量机解决。
  5. 随着样本点增多，拉格朗日系数求解困难。

参考

CATALOG
    FEATURED TAGS
    LPCNet Vocoder python gcc make makefile cmake TTS Front End Polyphone Disambiguation mask vector BERT knowledge distillation TinyBERT
    FRIENDS