LSTM
理解:输入门,遗忘门,输出门 在0到1之间,候选记忆细胞在-1到1之间。候选记忆细胞代表的是当前的短期记忆,输入门代表的是多少短期记忆或者说候选记忆输入到记忆细胞; 遗忘门代表的是遗忘上一个记忆细胞带来的长期记忆;输出门代表的当前的输出。需要注意,候选记忆细胞代表的是短期记忆,上一个时刻的记忆细胞代表的是长期记忆,通过遗忘门和输入门来控制短期记忆和长期记忆。
LSTMCell运算:
GRU
理解: 重置门在计算候选记忆细胞使用,理解为重置之前的记忆。如果重置门为1,R和H_t-1按元素相乘结果是H_t-1,候选记忆细胞会保留之前的记忆;如果重置门为0,R和H_t-1按元素相乘结果是0,候选记忆细胞会彻底遗忘之前的记忆;更新们在计算H的时候使用,它用来计算上一个隐藏状态有多少信息被保留下来,且新的内容(候选记忆细胞)有多少需要被添加(被记忆),更新门为1,候选记忆细胞会全部流入当前的H,并且不会保留上一时刻隐藏状态;更新们为0,会完全保留上一时刻隐藏状态,并且不会保留记忆细胞。
注意: 上一时刻隐藏状态在流入到当前时刻隐藏状态时,要经过重置门去求解候选记忆细胞,同时也会经过更新门去求解多少上一时刻隐藏状态被更新到下一时刻隐藏状态。
注意:在运算时,tensorflow等通常是把循环单元,非循环单元作为整体参与运算。以keras为例,gru的参数为[[W_xz,W_xr,W_xh],[W_hz,W_hr,W_hh],[b_z,b_r,b_h]]或者[[W_xz,W_xr,W_xh],[W_hz,W_hr,W_hh],[[b_xz,b_xr,b_xh],[b__hz,b_hr,b_hh]]],即把三个非循环单元cat在一起,三个循环单元cat在一起,三个偏置cat在一起参与运算。实例中给了两个版本是根据:循环单元和非循环单元是否共享偏置(由reset_after参数控制)。
Attention
e.g.
AttentionCell运算:
CNN
Conv2d
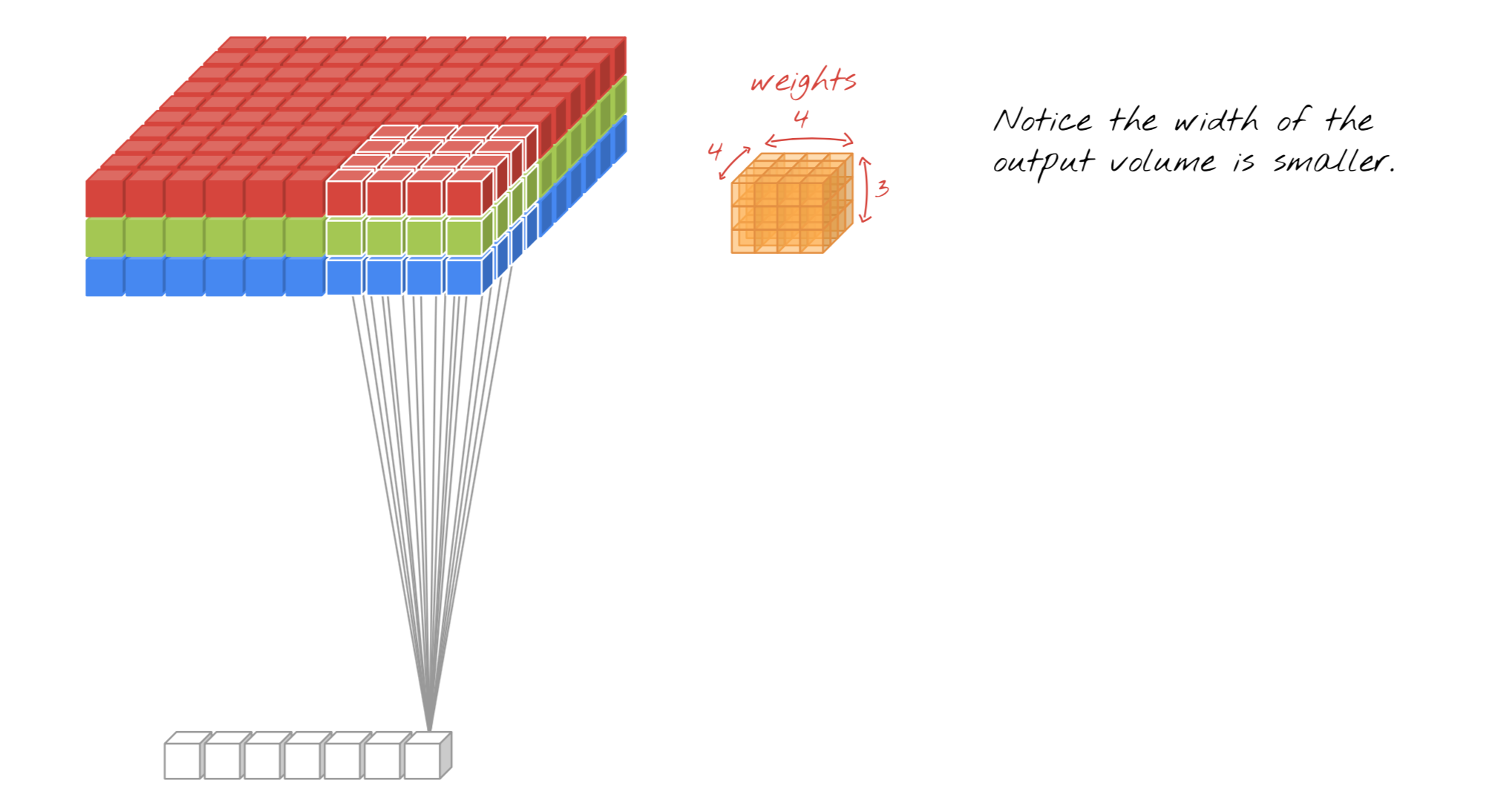
Input:10x10x3(长x宽x输入维度)
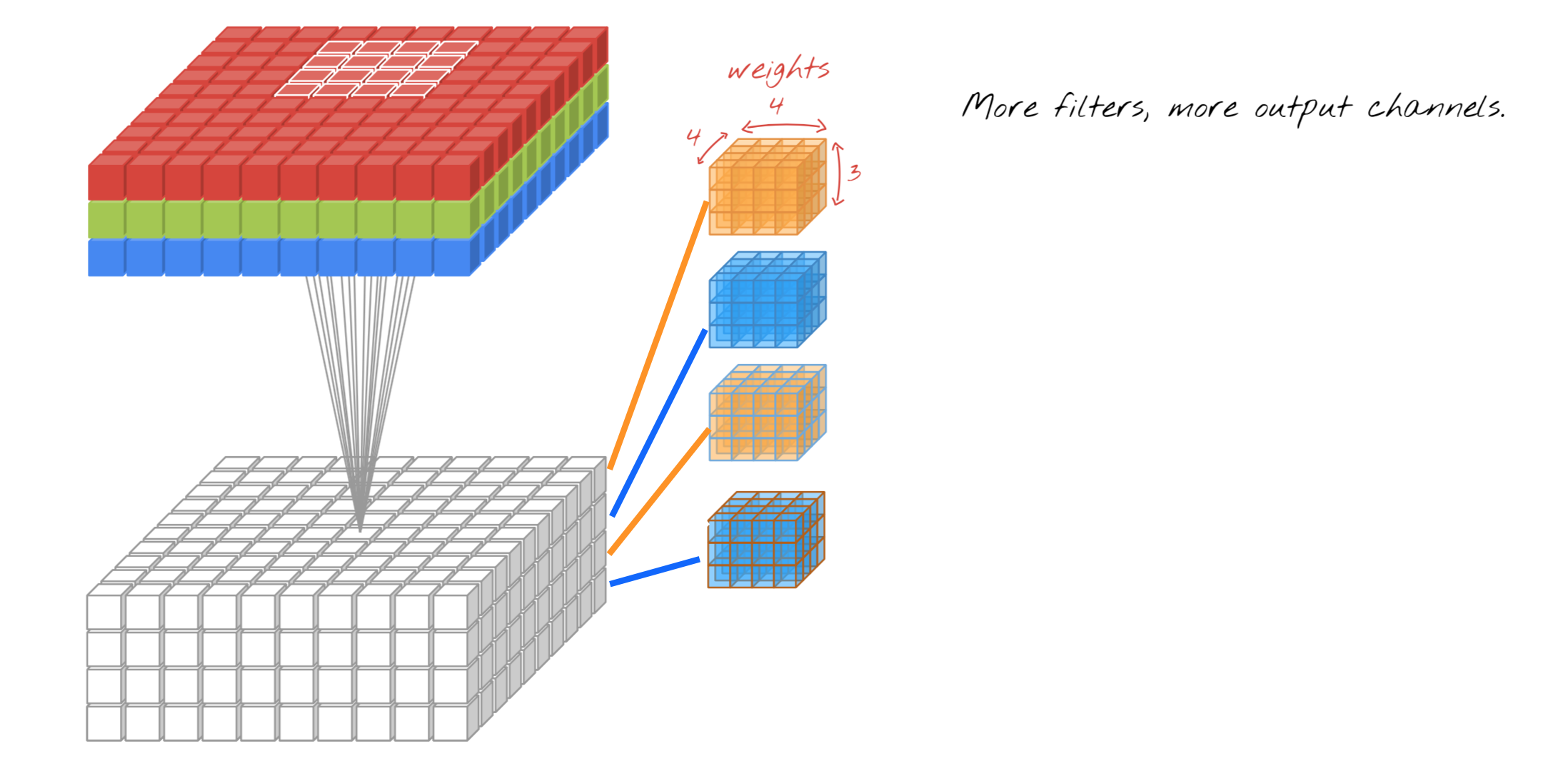
Filters(output channel or滤波器数量or输出维度or输出深度):4
kernel size(卷积核尺寸):4x4
Stride:1
Weights:4x4x3x1(卷积核尺寸x输入维度x输出维度)
Output:10x10x4("SAME") or (10-4+1)x(10-4+1)x4("VALID")
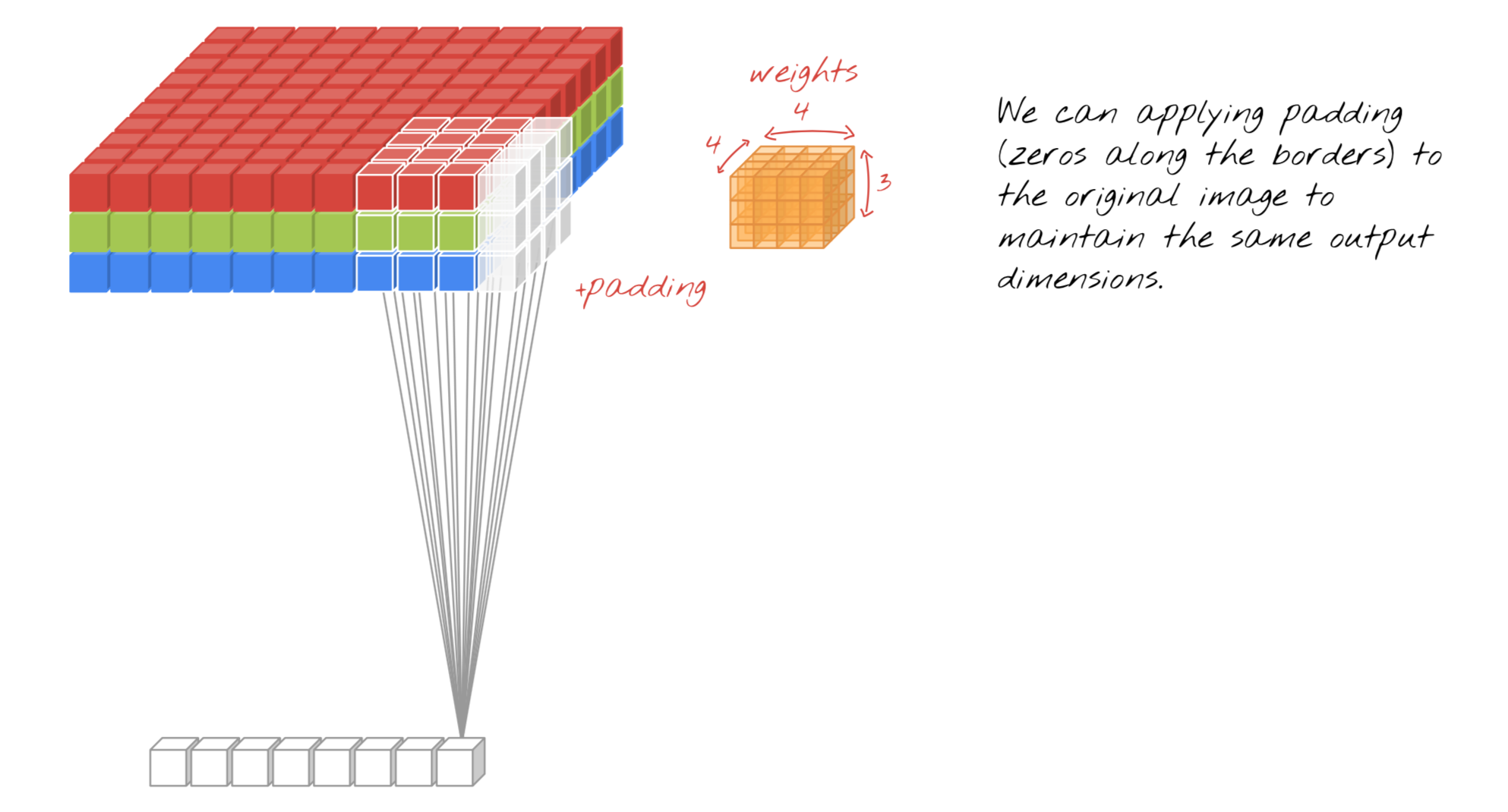
Pool2d
AvgPool2d or MaxPool2d
Conv1d
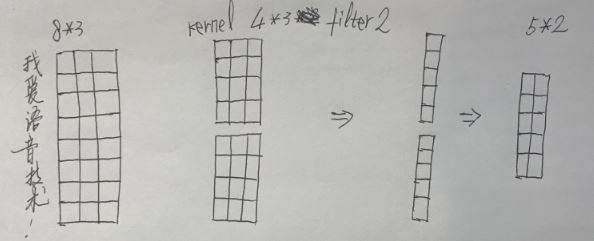
Input:8x3(句子帧数x每帧的维度)
Filters(output channel or滤波器数量or输出维度or输出深度):2
kernel size(卷积核尺寸):4
Stride:1
Weights:4x3x2(卷积核尺寸x输入维度x输出维度)
Output:8*2("SAME") or (8-4+1)*2("VALID")
Pool1d
AvgPool1d or MaxPool1d
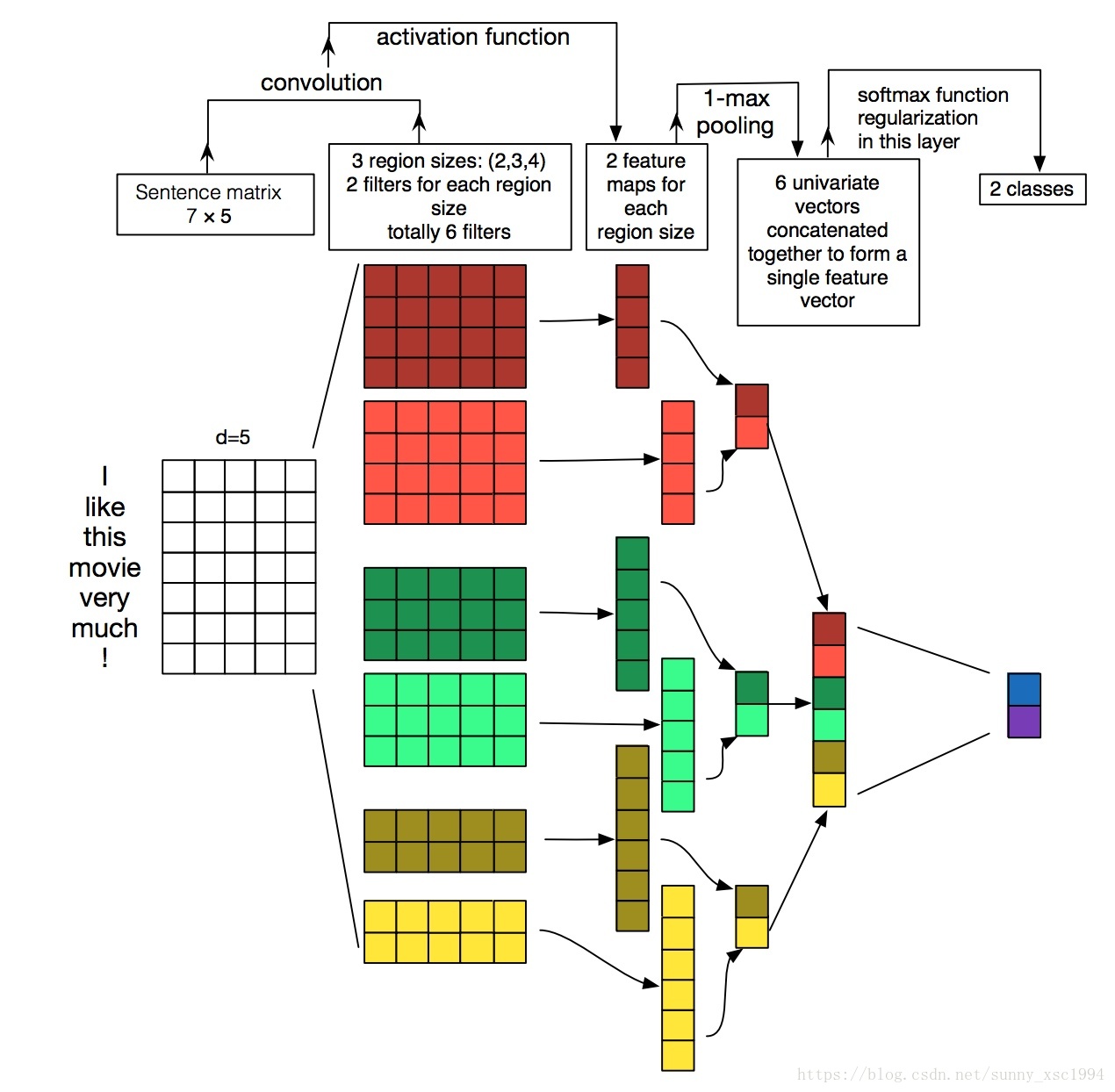
语音技术中常用的1D技法:concat不同卷积核大小的输出结果
Input:7x5(句子帧数x每帧的维度)
Filters(output channel or滤波器数量or输出维度or输出深度):for i in 2,2,3,3,4,4
kernel size(卷积核尺寸):1
Stride:1
Weights:2x5x1,2x5x1,3x5x1,3x5x1,4x5x1,4x5x1(卷积核尺寸x输入维度x输出维度)
Max pooling and the first time concat 0utput:2x1,2x1,2x1
After second concat:6x1
Output:2x1
Transpose Conv2D
Transpose Conv1D
语音合成中使用转置卷积,我们需要控制samples的长度.
torch.nn.ConvTranspose1d(in_channels, out_channels, kernel_size, stride, padding, output_padding, groups, dilation, padding_mode)
当我们想要Lout为Lin的M倍时,只需设置stride=M,然后解出其他参数即可。
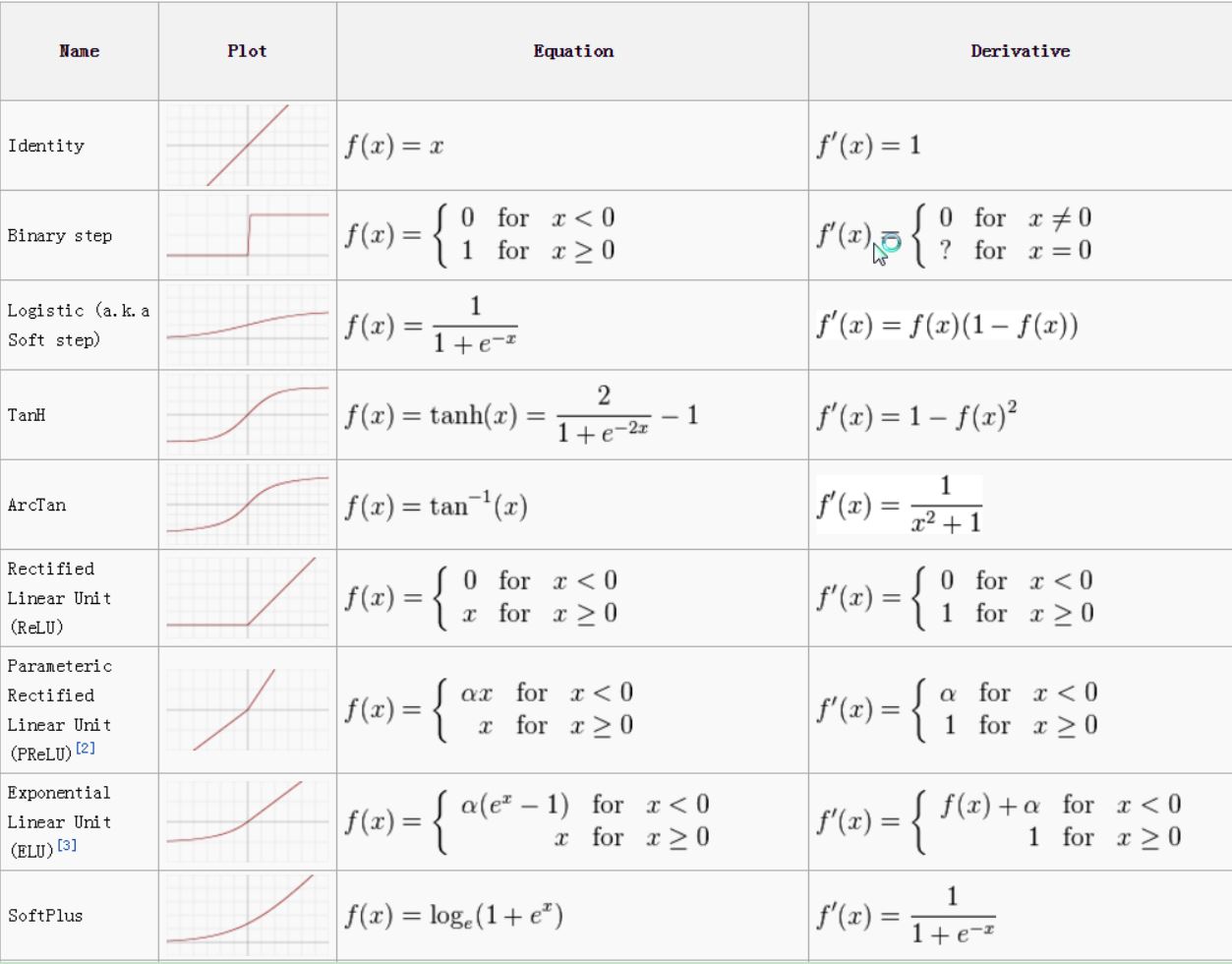
Activation fuction
学习率曲线的warmup设置
def _learning_rate_decay(init_lr, global_step):
# Noam scheme from tensor2tensor:
warmup_steps = 4000.0
step = tf.cast(global_step + 1, dtype=tf.float32)
return init_lr * warmup_steps**0.5 * tf.minimum(step * warmup_steps**-1.5, step**-0.5)
其中global_step=tf.Variable(0, trainable=False),每次一个minibatch后自动加一。学习率是伴随global_step的变化而变化的。
warmup的设置可以看出,学习率曲线是在global_step在warmup之前单调递增,在warmup时到达峰值,随后单调递减。
这么做的好处是,如果训练开始模型还没有见过所有的数据的时候就以高学习率进行学习,可能会陷入鞍点。
warmup的设置,个人的经验是两到三个batch。
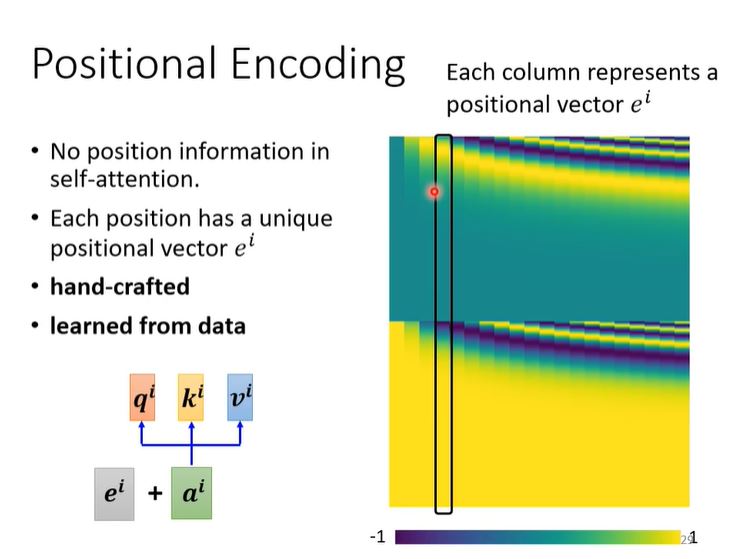
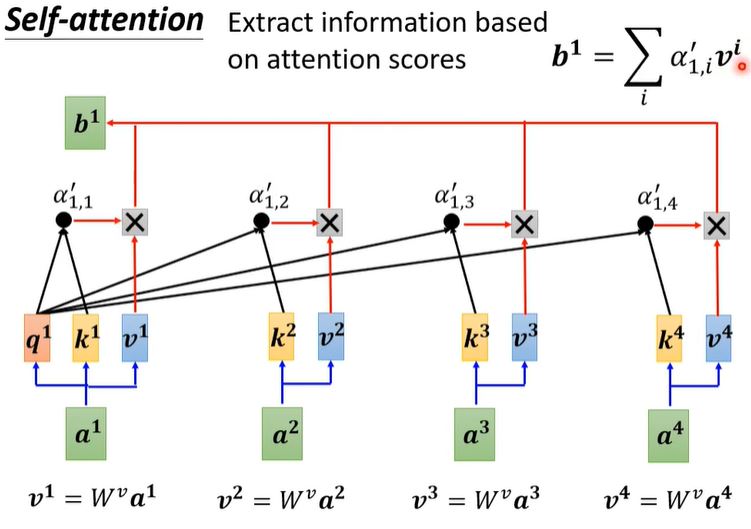
self attention(李宏毅)

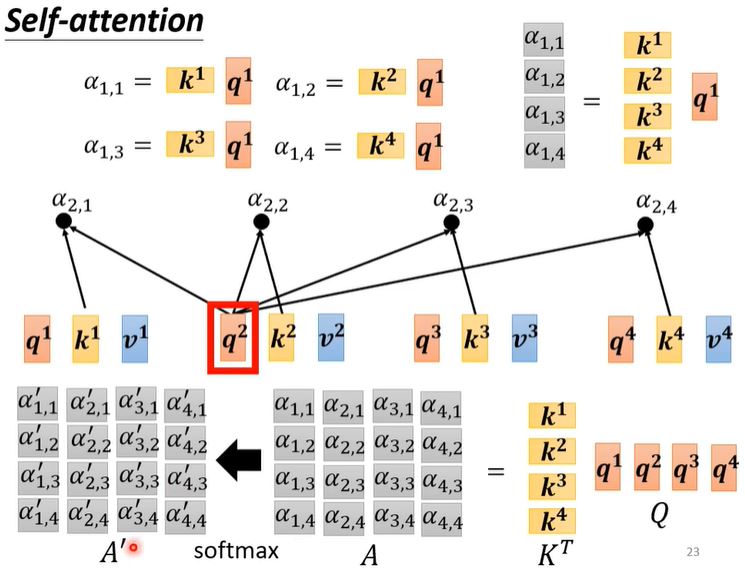
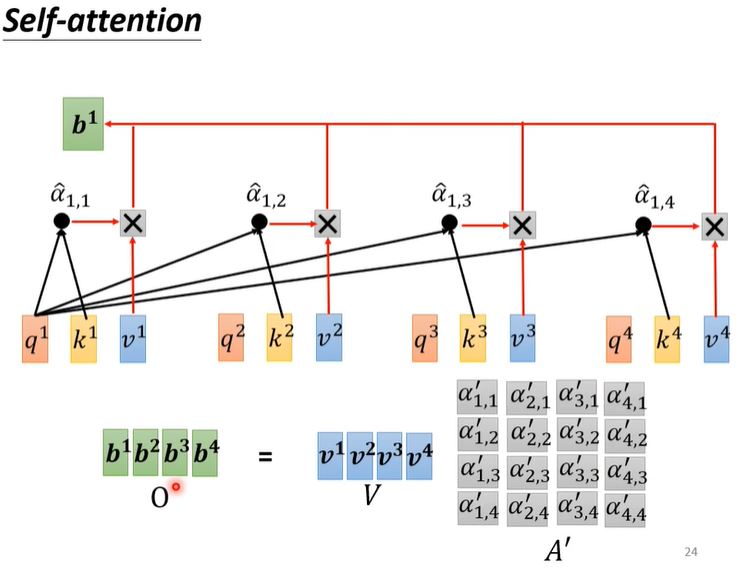
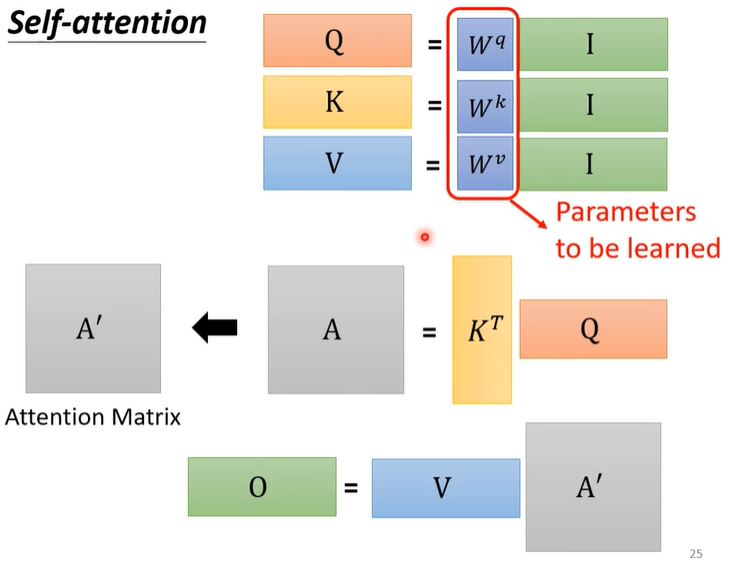
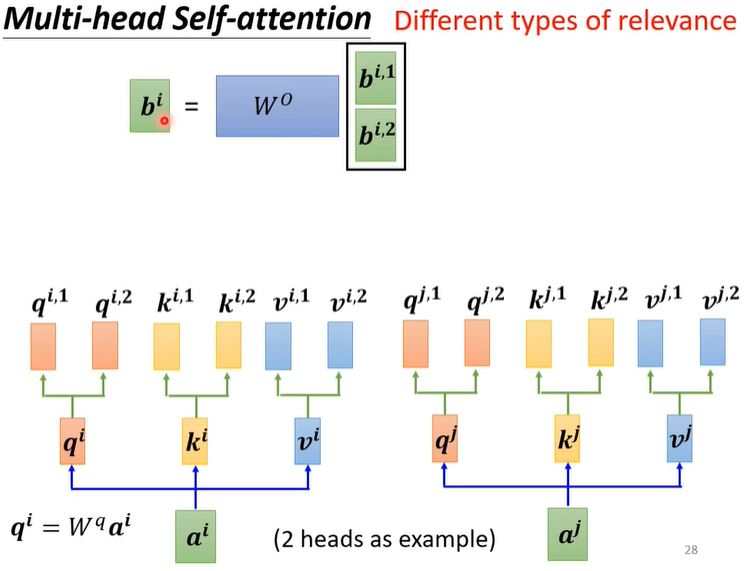
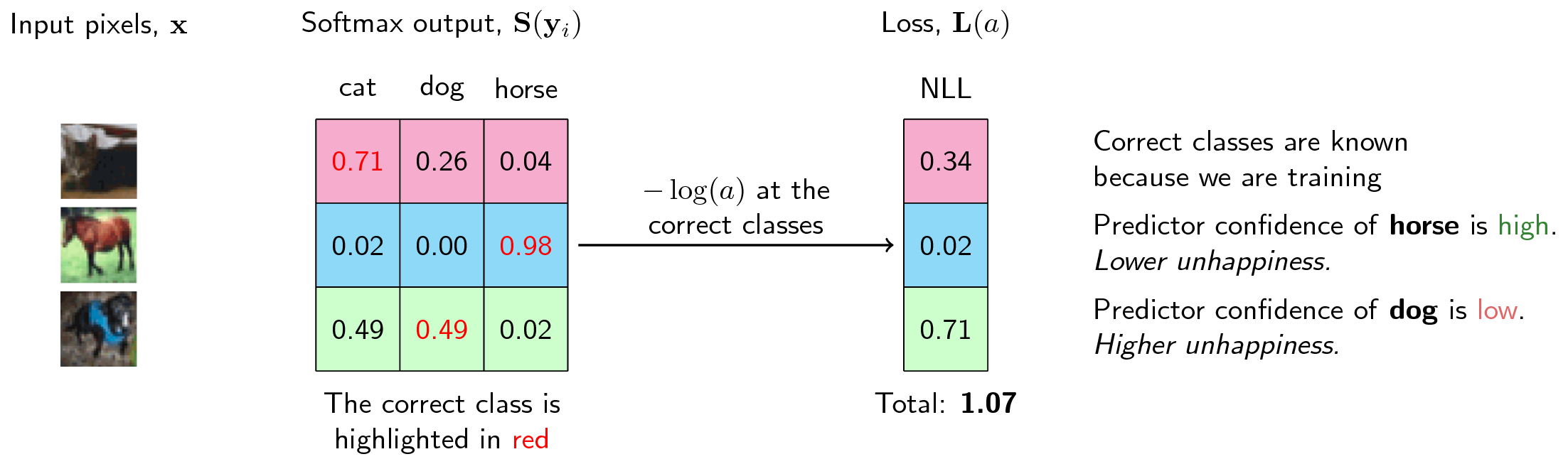
Negative Log-Likelihood (NLL)
L(y)=−log(y)
实践中,softmax函数通常和负对数似然(negative log-likelihood,NLL)一起使用,本质是对正确的标签的预测概率取-log()运算,因此正确标签预测概率越大,其数值越小,我们的NLL损失函数就是要最小化这个值(也就是最大化正确类别标签的概率预测值)

python脚本的执行过程
过程概述:
词法分析—>语法分析—>编译字节码文件—>执行
词法分析:关键字是否有误。
语法分析:语法是否有无。
编译字节码文件:python中有一个内置函数compile(),其具体为compile(source,filename,mode)。它可以将源文件编译成codeobject。import dis模块进行反编译,发现python字节码其实是模仿的x86的汇编,将代码编译成一条一条的指令交给一个虚拟的cpu去执行
字节码是python虚拟机程序里对应的PyCodeObject对象。.pyc文件时字节码在磁盘上的表现形式。简单来说就是在编译代码的过程中,首先会将代码中的函数,类等对象分类处理,然后生成字节码文件。
有了字节码文件,CPU可以直接识别字节码文件进行处理,接着python就可以执行。
修改.pyc文件不会对python的执行结果有影响,每次运行的时候都会覆盖修改的地方。
c程序的执行过程
过程概述:
预处理—>编译—>汇编—>链接
预处理(preprocessing):include头文件以及宏定义替换成其真正的内容,预处理之后得到的仍然是文本文件,但文件体积会大很多。gcc -E -I./inc test.c -o test.i 生成.i文件。
编译(compilation):将经过预处理之后的程序转换成特定汇编代码(assembly code)的过程,gcc -S -I./inc test.c -o test.s 生成.s汇编文件。
汇编(assemble):汇编过程将上一步的汇编代码转换成机器码(machine code),这一步产生的文件叫做目标文件,是二进制格式。gcc -c test.s -o test.o 生成.o二进制机器码文件。
链接(linking):链接过程将多个目标文以及所需的库文件(.so等)链接成最终的可执行文件(executable file)。gcc hello.c -o test.out 后生成.out可执行文件。
python decorators
装饰器本质上是一个Python函数或类,它可以让其他函数或类在不需要做任何代码修改的前提下增加额外功能,装饰器的返回值也是一个函数/类对象.装饰器的作用就是为已经存在的对象添加额外的功能.
装饰器传入的参数是function,返回值也是这个function。添加的额外功能在装饰器方法里面。
</pre>
def use_logging(func):
def wrapper():
logging.warn("%s is running" % func.__name__)
return func() # 把 foo 当做参数传递进来时,执行func()就相当于执行foo()
return wrapper
def foo(): print(‘i am foo’)
foo = use_logging(foo) # 因为装饰器 use_logging(foo) 返回的时函数对象 wrapper,这条语句相当于 foo = wrapper foo() # 执行foo()就相当于执行 wrapper() </pre>
@是装饰器的语法糖
def use_logging(func):
def wrapper():
logging.warn("%s is running" % func.__name__)
return func()
return wrapper
@use_logging #语法糖的含义是: foo = use_logging(foo)
def foo():
print("i am foo")
foo()
@property decorators 和 func.setter , func.getter
本质是:使用装饰器实现对属性进行控制。 把一个getter方法变成属性,只需要加上@property就可以了
归一化(标准化)以及批量归一化(BN)
z-score标准化:原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1。
反归一化:
批量归一化(BN):以mini-batch为单位对数据进行whitening preprocessing可以加快训练以及收敛
其中γ和β都是可训练参数。有趣的是,若是人为控制该组参数,可以控制神经网络的输出风格(例如可以进行讲话风格或者绘画风格的学习)。
MinMaxScaler标准化
基本公式:
scale:[min,max]是标准化后的范围
逆变换时需要的数据:
Transform:
inverse transform:
声音与信号
一小段音频经离散余弦变换DCT(通常是采用FFT)得到频谱spectrum。横坐标频率,纵坐标可以是振幅也可以是相位。 短时傅里叶变换STFT:对整段音频进行加窗,对每窗音频进行DCT(FFT)。 对整段音频进行短时傅里叶变换得到线性谱,是复数。对线性谱取绝对值np.abs() 得到线性振幅频率谱magnitude of frequency,取np.angle()得到线性相位频率谱phase of frequency。 对线性幅频谱平方得到 线性幅频功率密度谱linear-frequency power spectral density(psd).
ctag + vim for cpp
ctags -R --c++-kinds=+p+l+x+c+d+e+f+g+m+n+s+t+u+v --fields=+liaS --extra=+q
vim中通过按键 Ctrl + ] 可以跳转到对应的定义位置,命令 Ctrl + o 可以回退到原来的位置. ctags –list-kinds=c++ 可列出C++支持生成的标签类型的全量列表.
c++内存管理
μ-law transform and inverse transform
μ-law transform: 首先把wav映射到(-1,1)
inverse transform:
CPU推理加速
- 指令集优化. -mavx2 -mavx512f
- 调用加速运算库. -lmkl-rt (Math Kernel Library,sigmoid激活函数、三角函数等的加速) -dnnl (矩阵乘加速)
- OpenMP使用多线程(Open Multi-Processing). -fopenmp
- 编译时的普通优化. -O3
- 16bit量化,INT8量化. 需要推理工具的软件支持以及cpu的硬件支持
- 网络稀疏化,网络裁剪