朴素贝叶斯假设
朴素贝叶斯是最简单的有向概率图模型,它的核心思想是条件独立性假设。
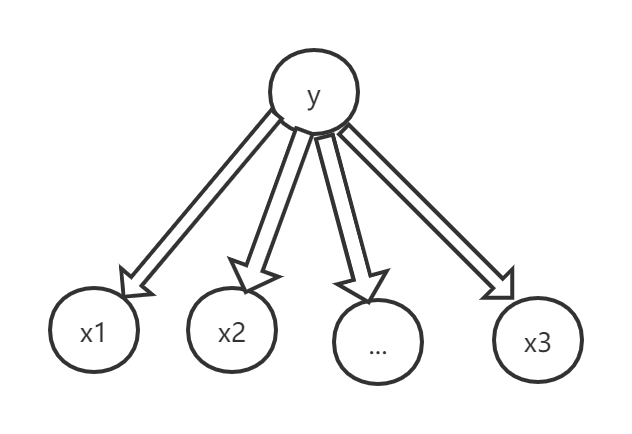
朴素贝叶斯假设:在给定类别的情况下,属性(特征)之间是相互独立的。
x是p维特征,y是类别,概率模型如下所示:
假设动机
朴素贝叶斯假设的动机是简化$P(x|y)$。
低维下似然可以直接计算,但是随着特征的维度增加,链式法则下似然的计算复杂度高,计算困难。
基于朴素贝叶斯假设:
从上式可以看出,贝叶斯假设解决了计算时的依赖链过长的问题,简化了特征的联合概率计算的复杂度。 同时我们也能够理解,基于同样目的的马尔可夫假设,比如HMM里的一阶齐次马尔可夫假设:${x_{j}}\bot{x_{i+1}}|x_{i},\forall{j<i}$,在给定当前状态的情况下,将来与过去相互独立,是更为宽松的假设。
朴素贝叶斯分类器
数据是data:
分类器的预测目标是:给定x情况下,预测y属于哪类。
由于:
因此:
朴素贝叶斯就是计算各类的先验概率,和各个类别下特征取值的条件概率,最后将各个类别下的特征取值条件概率相乘,并乘上该类别的先验概率,取乘积最大的对应的类别作为预测类别。 基于不同特征分布,我们可以采用不同的模型(多项式模型,高斯模型,伯努利模型)。 高斯模型:
技术处理
- 平滑处理 为了防止某个特征的似然为0的情况,会导致联合概率也为0,因此进行平滑处理。
其中, $\alpha$=1称为Laplace平滑,$\alpha\in{(0,1)}$时为Lidstone平滑,M为所有特征的总数。
- 对数运算 面对连乘的计算,引入对数是自然而然的操作。
例子
使用贝叶斯估计判断是否新型冠状病毒感染者。
数据集中有六人,其中感染者三人,未感染者三人。
| 序号 | 发烧 | 咳嗽 | 无精神 | 感染 |
|---|---|---|---|---|
| 1 | 是 | 否 | 是 | 是 |
| 2 | 是 | 是 | 否 | 是 |
| 3 | 否 | 是 | 是 | 是 |
| 4 | 否 | 否 | 否 | 否 |
| 5 | 否 | 否 | 是 | 否 |
| 6 | 否 | 是 | 否 | 否 |
给定一人:发烧,不咳嗽,有精神,判断是否为新型冠状病毒感染者。
分析:x是三维的特征,分别是{发烧,咳嗽,无精神},y是类别,{感染者,未感染者}。注意观测未感染者时发烧的概率为0。
计算先验:
计算似然:
推断(例子简单不需要对数运算更清晰):
因此推断结果时给定一人:发烧,不咳嗽,有精神,则该人为感染者的几率大。
代码
上述例子给出了特征离散模型,下面给出连续型。连续型特征我们一般采用高斯模型。python代码摘自GitHub。
class NaiveBayes():
def fit(self, X, y):
self.X = X
self.y = y
self.classes = np.unique(y)
self.parameters = {}
for i, c in enumerate(self.classes):
X_Index_c = X[np.where(y == c)]
X_index_c_mean = np.mean(X_Index_c, axis=0, keepdims=True)
X_index_c_var = np.var(X_Index_c, axis=0, keepdims=True)
parameters = {"mean": X_index_c_mean, "var": X_index_c_var, "prior": X_Index_c.shape[0] / X.shape[0]}
self.parameters["class" + str(c)] = parameters
def _pdf(self, X, classes):
eps = 1e-4
mean = self.parameters["class" + str(classes)]["mean"]
var = self.parameters["class" + str(classes)]["var"]
numerator = np.exp(-(X - mean) ** 2 / (2 * var + eps))
denominator = np.sqrt(2 * np.pi * var + eps)
result = np.sum(np.log(numerator / denominator), axis=1, keepdims=True)
return result.T
def _predict(self, X):
output = []
for y in range(self.classes.shape[0]):
prior = np.log(self.parameters["class" + str(y)]["prior"])
posterior = self._pdf(X, y)
prediction = prior + posterior
output.append(prediction)
return output
def predict(self, X):
output = self._predict(X)
output = np.reshape(output, (self.classes.shape[0], X.shape[0]))
prediction = np.argmax(output, axis=0)
return prediction
总结
- 贝叶斯条件独立性假设下,极大的简化了联合概率的计算,提高了效率。
- 现实世界中特征间的关系不是独立的,一般情况下很难满足朴素贝叶斯假设,贝叶斯假设太过理想化。